 |
| 眠れぬ夜のために。 小学校程度の算数をたのしんでみる。 |
|
1.まずは小手調べの問題ですね。 オレンジ色で書いた線が同じ長さだってことに 気づきましたか? 辺AB と 辺A'B はもともと半円の同じ部分ですから、 両方とも 16cm です。 この二等辺三角形をよく見ると、 角BAA' と 角BA'A は同じ大きさです。 三角形の3つの角の大きさを合計すると 180°なので 角X の大きさは (180-45)÷2 = 67.5 °となります。 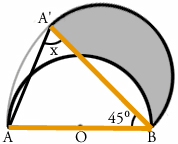 2.灰色の線の部分は、点B を中心とする 半径16cm の円の一部です。 直径 X 3.14 が円周の長さですから、 大きな円の円周の長さは 16 X 2 X 3.14 = 100.48cm 灰色の線の部分は円が 360°あるうちの 45°ぶんなので 100.48 X 45/360 = 12.56cm となります。 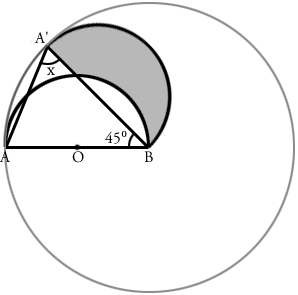 この問題、横着をして16cmを2倍せずに6.28cm なんていう 答えを出した人が結構いるんじゃないかと思うんですが、 どうですか? できましたか? 3.灰色の部分は 辺A'B を直径とする半円から青い部分を 引いた残りの部分です。ここまではわかりますよね。 この青い部分の面積が求められるかどうかが 解けるかどうかの分かれ目です。 下にオレンジ色で書いた補助線、書けましたか? 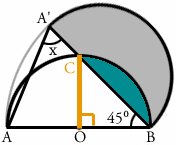 こうやって補助線を引けば、 青い部分が、円の一部から三角形OCB を引いた残りだという ことがわかります。 パイ型の部分(円の一部)の面積は 8 X 8 X 3.14 X 90/360 = 50.24cm2 三角形OCBの面積は 8 X 8 X 1/2 = 32cm2 なので、青い部分の面積は 50.24 - 32 = 18.24cm2 となります。 A'Bを直径とする半円の面積は 8 X 8 X 3.14 X 180/360 = 100.48cm2 ですから、求める面積は 100.48-18.24 = 82.24cm2となります。 3番までできた方おめでとうございます。 今回は途中で面倒になって答えを見ちゃった人が 結構いるかもしれませんね。 次回はもっと計算が楽な問題を選んでみます。 |
1999-04-16-FRI
 戻る |